Распоред са најмањим закашњењем

Радник треба да заврши \(n\) послова. За сваки од послова које треба завршити познато је трајање у минутима и рок до којег се посао мора завршити. Радник почиње да ради у тренутку 0, започете послове ради док их не заврши и не може да ради два посла истовремено. Ако се посао не заврши у предвиђеном року, муштерије ће бити незадовољне. Што је кашњење веће, веће је и незадовољство. Ако је нека муштерија баш јако незадовољна, престаће да наручује послове у овој фирми. Зато послове треба распоредити тако да, ако је то могуће, не постоји ниједна муштерија која је баш јако незадовољна (боље је имати више мало незадовољних муштерија, него једну много незадовољну). Зато се укупан квалитет распореда послова одређује на основу највећег направљеног закашњења – потребно је да оно буде што мање. Написати програм који одређује оптималан распоред, тј. највеће кашњење неког посла у том распореду.

Улаз

Са стандардног улаза се у првом реду уноси број \(n\) (\(1 \leq n \leq 10^5\)), затим у наредном реду трајања послова \(t_i\) (позитивни цели бројеви) и затим у наредном реду рокови за завршетак послова \(r_i\) (позитивни цели бројеви).

Излаз

На стандардни излаз исписати квалитет најбољег распореда (највеће направљено закашњење у том распореду).

Пример

Улаз

6
1 2 2 3 3 4
9 8 15 6 14 9

Излаз

1

Објашњење

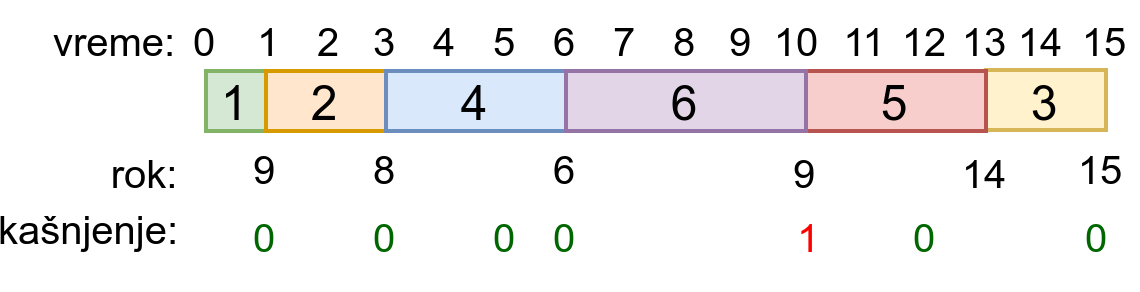
На слици је приказан један распоред послова код којег је највеће кашњење једнако 1 (само се посао број 6, који треба да се заврши у 9 завршава један минут касније, у 10).